Field and temperature dependence of the skyrmion lattice phase and the appearance of a second helical phase in FeGe
D.M. Burn, S.L. Zhang, T. Hesjedal and G. van der Laan
Magnetism and Magnetic Materials Online November 2020
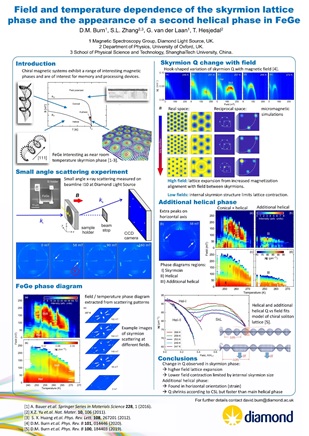
FeGe is a noncentrosymmetric helimagnet exhibiting non-collinear spin textures. Below the ordering temperature, Tc, bulk FeGe has a well-established and rich magnetic phase diagram showing helical, conical, and skyrmion states [1]. The skyrmion pocket has a wide, layer thickness dependent, temperature vs. field window extending up to room temperature [2-4]. These features make FeGe of great interest due to the potential for novel room-temperature devices based on the manipulation of topological magnetic states.
Here, we characterize the magnetic states in a thin membrane of FeGe with small angle soft x-ray scattering as a function of both temperature and out-of-plane magnetic field. We reveal a hook-shaped dependence of the modulation vector on the applied field whilst traversing the skyrmion phase pocket. This dependence arises due to competition between changes in the skyrmion size and packing density that occur as a function of field [5].
In addition to the helical, conical, and skyrmion phases, we observe an additional helical phase which coexists beneath the skyrmion phase in the phase diagram, towards the higher field boundary of the helical phase. In contrast to the other phases this additional helical phase shows strong uniaxial preferential alignment of the modulation vector [6].
Our findings build upon other work on FeGe, strengthening the case that the room-temperature topological magnetic properties are of great interest for the development of novel technological devices. Our work shows how multiple coexisting phases can be simultaneously and uniquely identified, which will provide further opportunities for potential information processing and storage methodologies.
[1] A. Bauer et.al. Springer Series in Materials Science 228, 1 (2016).
[2] X.Z. Yu et.al. Nat. Mater. 10, 106 (2011).
[3] H. Wilhelm et.al. J. Phys.: Condens. Matter 24, 294204 (2012).
[4] S. X. Huang et.al. Phys. Rev. Lett. 108, 267201 (2012).
[5] D.M. Burn et.al. Phys. Rev. B 101, 014446 (2020).
[6] D.M. Burn et.al. Phys. Rev. B 100, 184403 (2019).